Go 64 bit

I decided recently to migrate my test C++ application (based on database flat files and Python interface) to 64 bit world keeping backward 32 bit compatibility and with minimal changes to code avoiding as much as possible branching the code with statements like that:

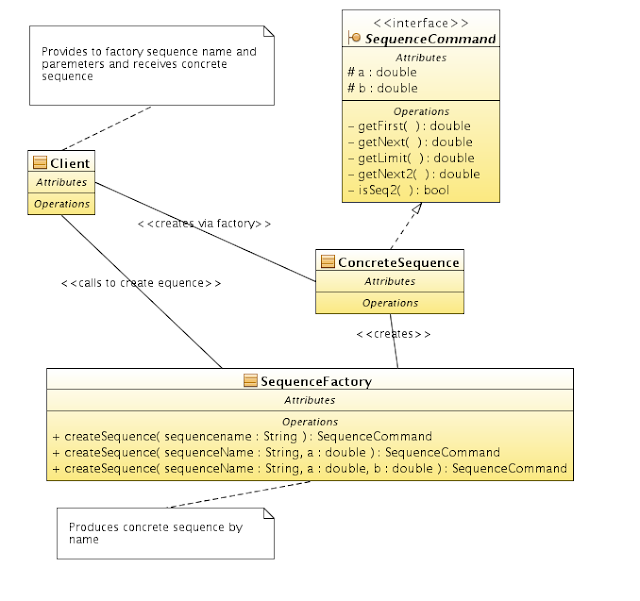
#ifdef 64BIT
.. something 64 bit specific
#else
.. something 32 bit specific
#endif

I achieved this goal but had to resolve the following problem.

Problem 1 : Code did not compile

#include <algorithm>
using namespace std;

unsigned int w;
.....
  max(w,sizeof(..));

The reason is quite simple, the sizeof operator is now 64 bit (unsigned long) so max template does not compile. In 32 bit version unsigned int and unsigned long are the same types. The solution is to use explicit conversion of one of the compared values.

Another solution could be to create custom MAX template:

template < class T1, class T2 >
T1 MAX( T1 x, T2 y ) {
  if ( x < y ) return y;
  return x;
}

But this solution could cause side effect if y>x - implicit conversion from T2 to T1. So I think that the better is explicit conversion.

Problem 2: Hard test that unsigned long is 4 bytes long.

In one piece was the test that unsigned long is 4 bytes long.

Something like:

config.h
...
#define SIZEOF_LONG 4

and somewhere in the code :

if (sizeof(usigned long) != SIZEOF_LONG) {
   throw error ....
}

The solution was to use (with heavy heart) conditional ifdef directive:

#ifdef BIT64
#define SIZEOF_LONG 8
#else
#define SIZEOF_LONG 4
#endif

 Problem 3: 32/64 file locking.

It took me some time to resolve another issue.

I needed simple mutex mechanism to allow only one process to do some administering task (like indexing common resources first time after installing). There are many synchronization methods available but to keep it as simple as possible I utilized lock mechanism on files.

Code snippet:

bool mutexOp(const std::string &semname,bool lock) {

   // use simple hash function for mapping string to number
   unsigned long no = 0l;
   for (int i=0; semname[i]; i++) no = (17*no) + (semname[i]-32);

   int lockfd;
   // get lockfd of file being used as semaphore

    struct flock fs;
    fs.l_type =  lock ? F_WRLCK : F_UNLCK;
    fs.l_whence = SEEK_SET;
    fs.l_start = no;
    fs.l_len = 1; // lock one byte only

    int res = fcntl( lockfd, F_SETLK, & fs );
    // ...........
    // analize res
}

According to Posix specification it is possible to lock bytes beyond the end of file so it works even having the "semaphore" file of 0 bytes long. But although off_t (type of l_start field) is 64 bit long the fcntl function does not work as expected for number grater than 2 ^ 32. On 32 bit machine unsigned long is 32 bit so hash function is automatically truncated to 32 bit, but on 64 bit it could be greater.
The solution is very simply, just do it yourself.

   unsigned long no = 0l;
   for (int i=0; semname[i]; i++) no = (17*no) + (semname[i]-32);
   no &= 0xffffffff;

Problem 4: Last but not least.

Application uses embedded indexed-sequential (ISAM) data base. One of the data types supported is 'unsigned long' keeping numbers 4 bytes long. 64 bit version should also support this 4 bytes unsigned longs to handle data bases created by 32 bit version. It was the problem I feared the most, it looked for me like an endless chain of fixing, patching, refactoring ... But there is also good news  that solution was very simple.

Application was originally designed that data base field types (int, long, double) could be differ than its counterpart in C++ program. So there is a common point of conversion between stream of bytes read from data base to C++ data types and vice versa and fix was very simple.

void convertStreamOfBytes(int fType, const void *sou, void *dest, bool todb)
{
  switch (fType) {
    case ...

    case ulongfield:
#ifdef BIT64
            if (todb) {
                *reinterpret_cast (dest) = *reinterpret_cast (sou);
            } else {
                *reinterpret_cast (dest) = *reinterpret_cast (sou);
            }
#else
            *reinterpret_cast (dest) = *reinterpret_cast (sou);
#endif
            break;
      case ...
   }
}

And it was all ! The design decision taken a long time ago pays off now !

Conclusion

So finally the goal was achieved. Application is 64 enabled, backward compatibility is kept and only few branchings inside the code.

But it is hard to say what real advantage it gives. The binaries are 10-15% greater. I don't think that it runs faster. Of course, I can address 64-bit space but this application is not memory thirsty. The only real advantage seems that it can be installed and run in pure 64 environment without necessity to install any 32 bit system components (e.g. 32 bit Python).

Welcome 64 bit world.

Programmer proof

I have been refreshing my math skills for some time. I'm reading on basics, limits of sequential. The limit can be finite, infinite or the sequence does not have a limit at all (is divergent). Sometimes the limit (finite or infinite) is obvious, sometimes it can be obtained by basic calculations, very often more advanced arithmetic should be applied to come to the conclusion.
I'm reading book (in Polish) http://pl.wikipedia.org/wiki/Grigorij_Fichtenholz G.M. Fichtenholz " Rachunek różniczkowy i całkowy"  and have come to the idea that pure math proof can be supported by "programmer proof", the program computing the numbers in the sequence and checking that the numbers are really getting closer to the limit. Of course, don't take "programmer proof" seriously, nothing can be proved that way.  But it can be useful to visualize how the sequence is running, the speed of convergence, or to start guessing on the limit.

Firstly it is necessary to create an architecture to define and run our sequences.

At the beginning let's define abstract class (interface) containing method signatures enabling polymorphic behavior for sequences.  Because very often sequence is defined recursively so more general methods 'getFirst' - 'getNext' are declared instead of 'getNthNumber'. This methods are pure virtual, there is no any defaults. Sometimes two sequences can be run at the same time so also methods for second sequence are declared with empty default definition. To emulate real numbers C++ double type is used.
Because very often recursive sequences use start values so also default constructors for 0, 1 or 2 start numbers are defined. Concrete sequence can also define custom constructor. Default constructors only set some const numbers at the beginning, it is up to concrete sequence to make use of it.

http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/seqcommand.h


This sequence interface is enough to create a simple sequence runner, the first draft of this runner simply goes 'N' times through sequence and prints results. Interface loaded with concrete sequence instance is an example of command pattern, it contains all data and methods sufficient to do task any time. Having parameters as const makes sure that we can come to initial state of the sequence every time.
Sequence runner contains one method to visualize (here to print) first N numbers in sequence. One can imagine more sophisticated visualizing method (e.g. graphic) or more complicated running algorithms e.g sampling sequence in intervals. Also some behavior of the sequence can be analyzed - e.g. how fast sequence is getting closer to its limit.

http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/seqengine.h

http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/seqengine.cpp

Because every sequence mimics the same interface factory design pattern proved to be very useful. This way the user should know the name of the sequence and initializing method (starting parameters). Factory produces proper sequence instance, the implementation is deeply hidden and not visible outside.

http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/seqcommandfactory.h

http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/seqcommandfactory.cpp

All sequences implemented so far are define here.

http://code.google.com/p/javahotel/source/browse/trunk/examples/#examples/sequence/sequences

The implementation is very simple, it is enough to keep all concrete methods inlined in header file.

Very high isolation level was achieved. Sequence runner can run through sequence using polymorphic behavior, does not have any access to implementation. Only sequence factory can create concrete sequence. The user can only create sequence by its name and run it using sequence runner.


Finally our architecture looks as follows.
Sequence command and sequence runner.

Sequence command and sequence factory.

And finally how client brings and binds them all:

Now look at several sequences:

Very simple sequence:

http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/sequences/seqharmcommand.h

That's obvious that the limit of this sequence is 0.

 Output

And it works ! This sequence really is getting close to 0.

Now more complicated sequence: (Fichtenholz, page 60)

http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/sequences/seqfih60.h
Assume : 0 < c < 1
and define sequence:

The limit of this sequence is 1.

Output

This sequence is approaching its limit very fast

Next sequence - arithmetic mean of two numbers.

(Fichtenholz - page 40)

http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/sequences/seq23command.h

The limit is equal to:

Output

Next sequence - Fihtenholz page 62

Take number a and define a sequence:

http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/sequences/seqc2.h

That's very interesting example of sequence, although the limit (if exists) is the same but the proof is different for different a.

For 0< a <=1  it can  be proved quite easily that limit is equal:

Output

For -3<=a<0 the limit is the same but the proof is more complicated because the sequence is not monotonic. It is monotonic for odd and even elements in the sequence.

Output

For a<-3 and a>1 the sequence is divergent, does not a limit at all. Example output for a = -3.1

Output

Next sequence - Fihtenholz page 60

http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/sequences/seqpower2.h

Sequence:


Assume 0<1

The limit of this sequence is 0.

Output

But this sequence is reluctant to achieve it's limit, milion object is still:

1000000 : 0.0005

Next sequence - Fihtenholz page 61

It is an example of two sequences running at the same pace. The first is arithmetic mean and the second harmonic mean of two numbers.

http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/sequences/seqavharm.h

Assume a>0 and b>0

The limit of this two sequences is the same and it is simply geometric mean of starting parameters:

Both sequences are getting close to the limit very fast.

Output