I'm reading book (in Polish) http://pl.wikipedia.org/wiki/Grigorij_Fichtenholz G.M. Fichtenholz " Rachunek różniczkowy i całkowy" and have come to the idea that pure math proof can be supported by "programmer proof", the program computing the numbers in the sequence and checking that the numbers are really getting closer to the limit. Of course, don't take "programmer proof" seriously, nothing can be proved that way. But it can be useful to visualize how the sequence is running, the speed of convergence, or to start guessing on the limit.
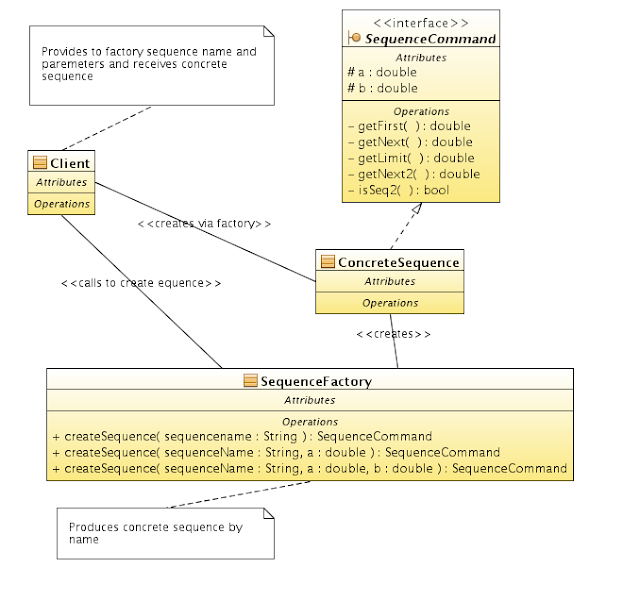
Firstly it is necessary to create an architecture to define and run our sequences.
At the beginning let's define abstract class (interface) containing method signatures enabling polymorphic behavior for sequences. Because very often sequence is defined recursively so more general methods 'getFirst' - 'getNext' are declared instead of 'getNthNumber'. This methods are pure virtual, there is no any defaults. Sometimes two sequences can be run at the same time so also methods for second sequence are declared with empty default definition. To emulate real numbers C++ double type is used.
Because very often recursive sequences use start values so also default constructors for 0, 1 or 2 start numbers are defined. Concrete sequence can also define custom constructor. Default constructors only set some const numbers at the beginning, it is up to concrete sequence to make use of it.
http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/seqcommand.h
This sequence interface is enough to create a simple sequence runner, the first draft of this runner simply goes 'N' times through sequence and prints results. Interface loaded with concrete sequence instance is an example of command pattern, it contains all data and methods sufficient to do task any time. Having parameters as const makes sure that we can come to initial state of the sequence every time.
Sequence runner contains one method to visualize (here to print) first N numbers in sequence. One can imagine more sophisticated visualizing method (e.g. graphic) or more complicated running algorithms e.g sampling sequence in intervals. Also some behavior of the sequence can be analyzed - e.g. how fast sequence is getting closer to its limit.
http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/seqengine.h
http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/seqengine.cpp
Because every sequence mimics the same interface factory design pattern proved to be very useful. This way the user should know the name of the sequence and initializing method (starting parameters). Factory produces proper sequence instance, the implementation is deeply hidden and not visible outside.
http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/seqcommandfactory.h
http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/seqcommandfactory.cpp
All sequences implemented so far are define here.
http://code.google.com/p/javahotel/source/browse/trunk/examples/#examples/sequence/sequences
The implementation is very simple, it is enough to keep all concrete methods inlined in header file.
Very high isolation level was achieved. Sequence runner can run through sequence using polymorphic behavior, does not have any access to implementation. Only sequence factory can create concrete sequence. The user can only create sequence by its name and run it using sequence runner.
Finally our architecture looks as follows.
Sequence command and sequence runner.
And finally how client brings and binds them all:
Now look at several sequences:
Very simple sequence:
http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/sequences/seqharmcommand.h
That's obvious that the limit of this sequence is 0.
Output
And it works ! This sequence really is getting close to 0.
Now more complicated sequence: (Fichtenholz, page 60)
http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/sequences/seqfih60.hAssume : 0 < c < 1
and define sequence:
The limit of this sequence is 1.
This sequence is approaching its limit very fast
Next sequence - arithmetic mean of two numbers.
(Fichtenholz - page 40)
http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/sequences/seq23command.h
The limit is equal to:
Output
Next sequence - Fihtenholz page 62
Take number a and define a sequence:
http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/sequences/seqc2.h
That's very interesting example of sequence, although the limit (if exists) is the same but the proof is different for different a.
For 0< a <=1 it can be proved quite easily that limit is equal:
Output
For -3<=a<0 the limit is the same but the proof is more complicated because the sequence is not monotonic. It is monotonic for odd and even elements in the sequence.
Output
For a<-3 and a>1 the sequence is divergent, does not a limit at all. Example output for a = -3.1
Output
Next sequence - Fihtenholz page 60
http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/sequences/seqpower2.h
Sequence:
Assume 0
The limit of this sequence is 0.
Output
But this sequence is reluctant to achieve it's limit, milion object is still:
1000000 : 0.0005
Next sequence - Fihtenholz page 61
It is an example of two sequences running at the same pace. The first is arithmetic mean and the second harmonic mean of two numbers.
http://code.google.com/p/javahotel/source/browse/trunk/examples/sequence/sequences/seqavharm.h
Assume a>0 and b>0
Both sequences are getting close to the limit very fast.
Output





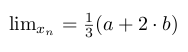





Brak komentarzy:
Prześlij komentarz